树
n个节点的树有n-1条边
n = n0+n1+n2
n-1 = n1+2*n2
BST
0度比全度的小1
数据结构中查找分为如下部分:
- 静态查找表: 顺序表(物)+二分(辑)
- 动态查找表 Tree + BST
- 哈希表及其查找
AVL
i层AVL最少结点数N[i] = N[i-1]+N[i-2]+1;
Huffman
从下往上建,取两个最小,0左1右
WPL = 权值*边长,累加。
R-B
根结点 叶结点(NULL)黑色
任一结点到叶结点遇到的黑色相同
一棵含有n个节点的红黑树的高度至多为2log(n+1)
如果一个节点是红色的,则它的子节点必须是黑色的
相对BST最长路径不大于两倍的最短路径的长度
相对AVL对平衡要求低,所以旋转次数少
数据比较乱是用红黑树,数据分布比较好用AVL
数据比较死就有hash,红黑树适合比较活的
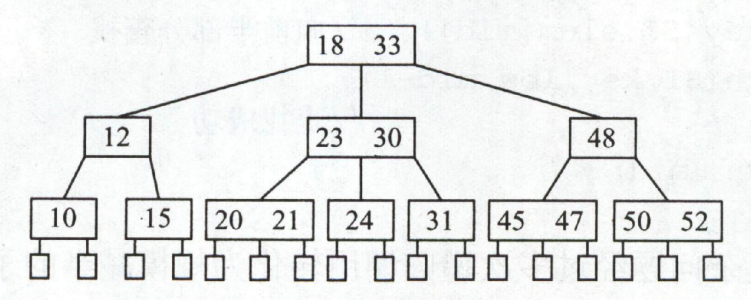
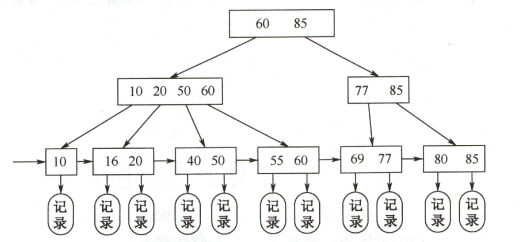
B/B+
- 每个结点是顺序表,树的遍历在磁盘,顺序表内的遍历在内存。
- O(lognN) 出度大于2
- B+非叶结点顺序表中各元素记录的是子结点的最大值,也就是会重复出现
- B+叶子结点顺序预读,空间局部性原理
堆
先层次遍历建立树,后从右下角adjust
for(int i=n/2; i>=0; i++) adjust(i). O(n)
pop后尾部移到头,adjust(1) O(logn), pop所有O(nlogn)
图表
hash
- 直接定址 y=ax+b
- 除留余数 y=x%p
- 数字分析 数码分布均匀的若干位(十百两位)
- 平方取中 平方值取中间
-
折叠 切割后累加
- 线性探测(next)
- 再散列(换另一个)
- 链地址法(遍历琏找key)
矩阵
邻接矩阵,n个结点,矩阵n*n
邻接琏表,n个结点,n条琏,该结点的邻结点相连
十字琏表,结点和弧,结点有两个指针指向in/out弧,弧有head/tail结点和两个指针,分别指向head/tail相同的弧,
路径
- 最小生成树 prim算法O(V^2)适合边密的
- 最小生成树 Kruskal算法O(eloge)边稀
- 最短路径 Dijkstra