介绍
- 监督学习：把样本分成具体的类，如邮件分类。
- 无监督学习：把样本分成若干类，不知道各类特性，如百度新闻分类
线性回归
- 方案：h(x) = θ’X
- 代价函数：J(θ) = 1/2m * sum[ (h(x) - y)^2 ]
- 梯度下降： θ = θ - a/m * ( θ‘X - Y )’X
正规方程
- θ = inv(X’X)X’Y
- 求逆O(n^3),适用于n<10000
- 正规方程仅用了线性回归
逻辑回归
- 方案：h(x) = 1/[1+exp(-θ’X)]，h’=h(1-h)
- 代价函数：
if y=1 -log(h(x))
if y=0 -log(1-h(x)) - 梯度下降： θ = θ - a/m*( θ‘X - Y )’X
- 分为多类时(y = 1 2 … n)
y=1为1类，y=其他为另一类，共两类，即化为2类问题
最后各类均有θ，求max(h(x))的索引
过拟合
- 方法
1.丢弃一些不能帮助我们正确预测的特征。
2.正则化(保留所有的特征,但是减少参数的大小) - 线性和逻辑
J = J + 入/2m*sum(θ) θ不包含θ0当不处罚θ0时
θ = (1-入/m)θ θ0 = θ0 - 正规方程
θ = inv(X’X-入ones(n+1,n+1))X’Y ones的（0,0）为0
神经网络
-
概念
基于逻辑回归，多类。各类均有1个向量θ，同理最后求其max(概率)。特别之处在于中间有递归多次。
比如1000样本分成10类，按逻辑回归思路，一步到位，而神经网络会把其先分为500,再把500分成100,最后10.
每步的样本输入为h(x),而非Xθ，否则经过多次递归肯定出错。
而逻辑回归只有一步 && h(x)单调增，故max(Xθ)效果同max(h(x))
当然，每步和输入的样本维度要+1
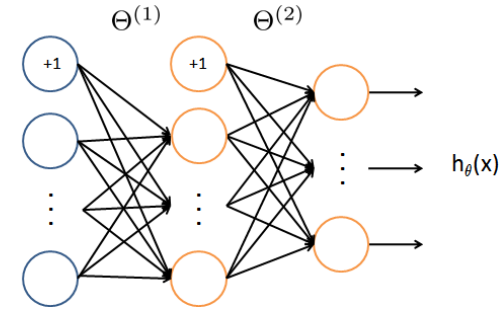
蓝圈x，红圈h(x) -
回归算法
a1 -> z2 -> a2 -> z3
a1 = [ones(m, 1) X]; %5000*401 1层准备输入2层
z2 = a1*θ1'; %5000*401 25*401 输入到2层的结果
a2 = [ones(m, 1) h(z2)]; %5000*26 2层准备输入3层
z3 = a2*θ2'; %5000*26 26*10 输入到3层的结果
h = h( z3 ); %5000*10 3层准备输出θ2_grad = (h-y)'* a2/m;
sigma2 = ((h-y)*θ2(:,2:end)).*hGrad( z2 );
θ1_grad = sigma2'* a1/m;当中间有一层网络时，
θ2_grad可简单的看成 (a2*θ2-y)^2对θ2求导，结果为 2*(h-y)*a2
θ1_grad可简单的看成(h(a1*θ1)*θ2-y)^2对θ1求导，结果为2*(h-y)*θ2 *h'(z2)*a1
当中间有两层网络时，
θ1_grad可简单的看成(h(h(a1*θ1)*θ2)*θ3-y)^2对θ1求导，结果为2h'(z3)*θ3*h'(z2)*θ2*a1
当中间3层时θ1_grad = 2h'(z4)*h'(z3)*h'(z2)*θ4*θ3*θ2*a1
实际上，是代价函数对θ求导。调参
- 欠拟合
入=0,维度=2
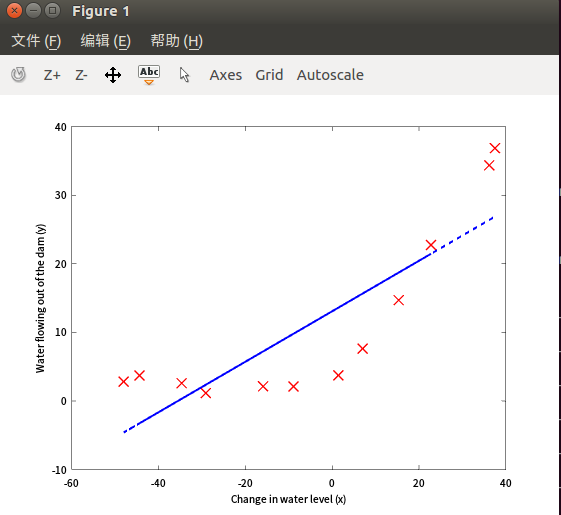
参数过少导致y值最终过大（欠拟合）
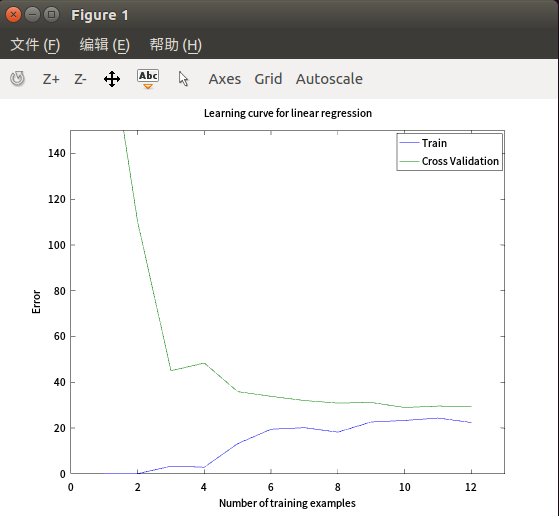
- 过拟合
扩大x的维度，入=0,维度=9
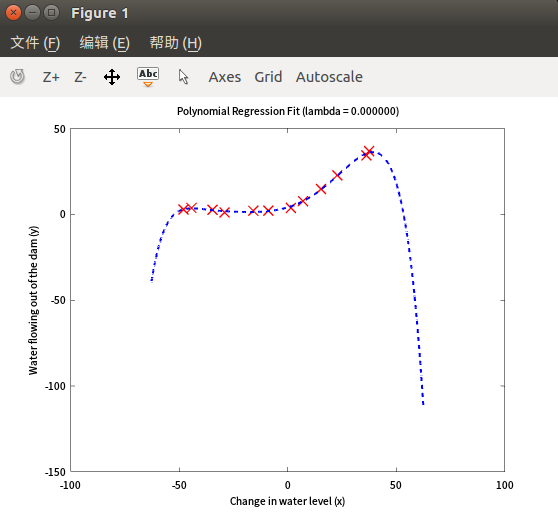
此时训练误差过小，过拟合
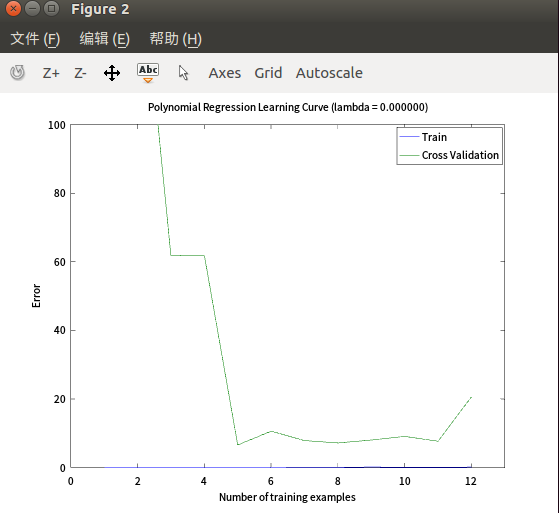
- 调整入
维度=9，样本数=max，入=1
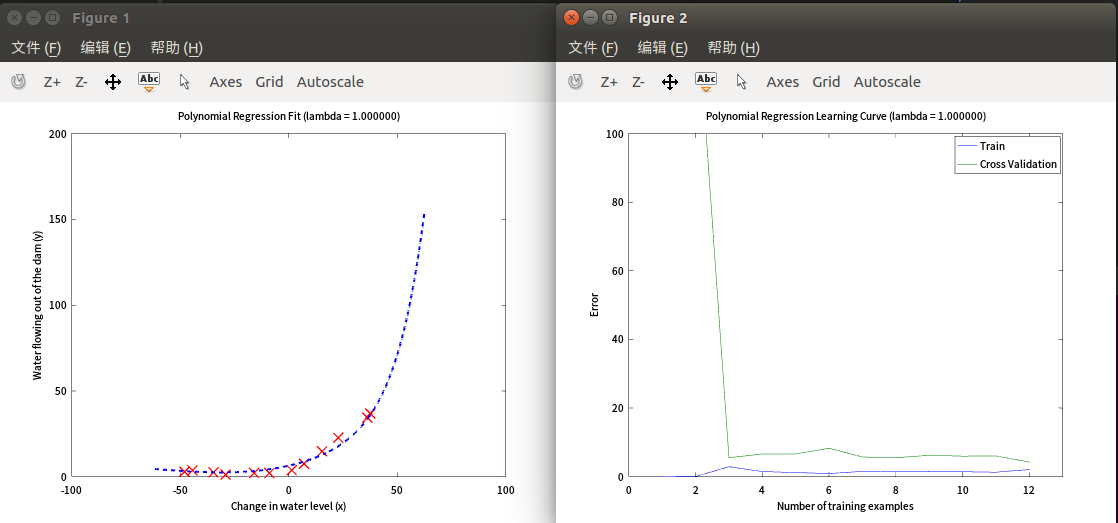维度=9，样本数=max，遍历入，发现3最合适
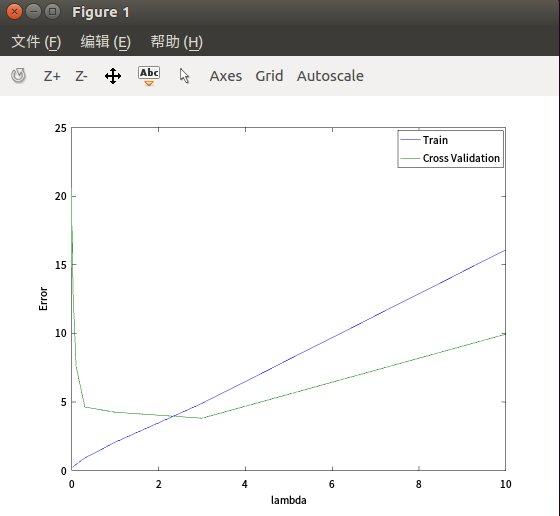
支持向量机
方案： y=1 if θ‘X>=1; y=0 if θ‘X<-1
代价函数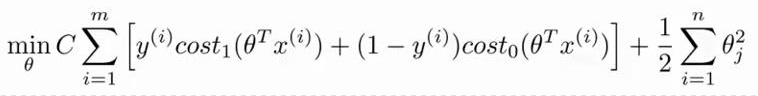 
C等同逻辑回归中的入，防止过拟合。
训练时会使θ‘X不处于（-1,1），比逻辑回归更严格。
因为分隔线与θ垂直，所以如果θ和X要更大，则θ和X要更同向，这分隔线更居中。
核函数
如果 x 维度过小，需要扩维。
-
高斯核函数
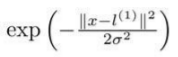
L是所有为样本点，如果有m个样本，则扩维成m，当然最后是m+1 -
线性核函数
保持原始维度