CSAPP笔记（六）存储器层次结构

RAM

随机访问存储器(Random-Access Memory)

SRAM

六晶体管，只要有电就能保持它的值

DRAM

对电容充电，需要不断的刷新
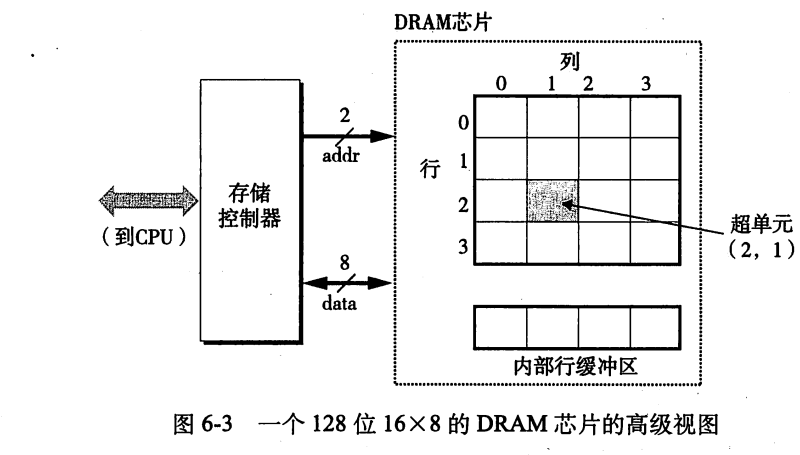
传统DRAM
4行4列共16个超单元，每个超单元有8个DRAM单元，也就是8位。
发送行地址2，第2行被读取到内部行缓冲区，再发送列地址1，（2，1）中的8位会输出。
采用行列式读写能减少引脚，但会增加时间，用时间换空间。

DDR SDRAM

双倍数据速率同步DRAM(Double Data-rate Synchronous DRAM, DDR SDRAM)，使用两个两个时钟缓冲沿作为控制信号，速递翻倍。

MM

存储器模块(Memory Module)

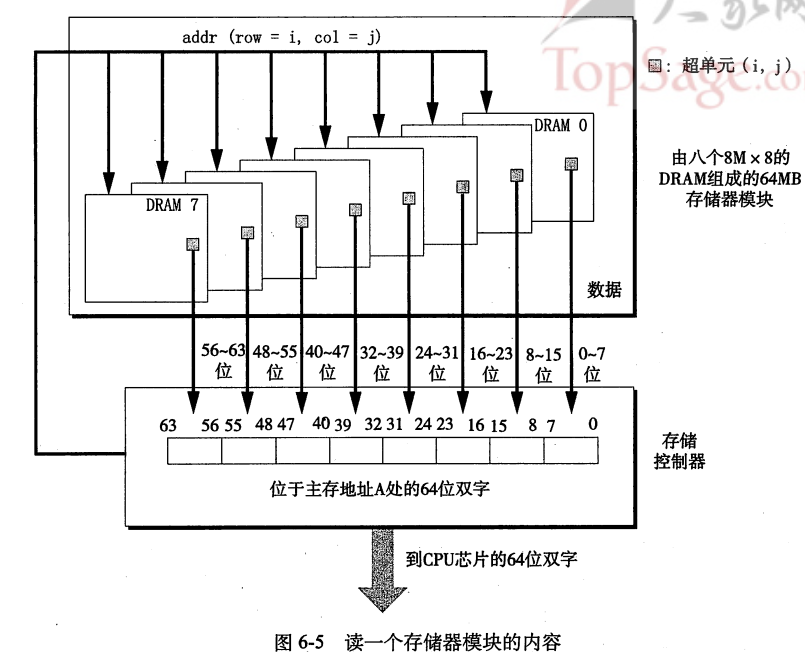
ROM

只读存储器(Read-Only Memory)，存储在ROM中和程序通常称为固件，比如BIOS。

PROM

Programmable ROM，可编程ROM，只能编程一次。

EPROM

Erasable Programmable ROM，可擦写可编程ROM，1000次

EEPROM

Electrically Erasable Programmable ROM，电子可擦除ROM, 100000次

闪存

闪存基于EEPROM，固态硬盘(Solid State Disk, SSD)基于闪存。

磁盘

多区记录

磁盘扇区间有隙，外环（柱面）间隙太大，故将n个柱面记为一个记录区，区中各环以最小环为准

磁盘控制器

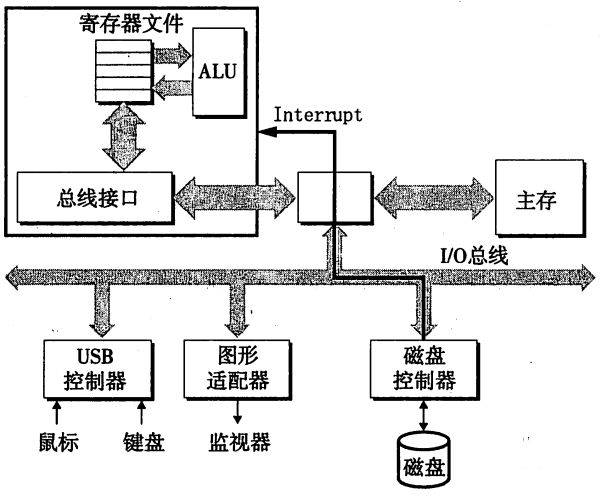
磁盘会占用一个IO端口（地址空间），CPU读取这个地址，告知逻辑块号与主存地址，磁盘控制器将操作系统要访问的逻辑块号翻译成物理的三元组（盘面，磁道，扇区），移动读写头，读到缓冲区，再到主存，申请中断。

缓存映射

缓存有n组，1组有n行，1行有一个块+一个标记+一个有效位。
CPU访问地址(01 0001 11)，记为（A,B,C）

直接映射

缓存16组，每组只有1行，A标记，B组号，C块内偏移。查找缓存上第B组上的标记是否为A且有效位为1,若是则读取第B组第1行的块的第C字节

组相映射

缓存8组2行,A+B前1为标记，B后3为组号，C偏移。组内自由。

全相映射

缓存16行，A+B为标记，组间自由。查找时遍历16行，找出标记为A+B的行。

换出策略

LRU

Least Recently Used
强调时间，不管以前被命中多少次，现在被命中了，优先级最高，最不可能被换出。
一旦被命中，计数段记为0，其他行加1。
值得注意的是，不命中时去加载新行，其他行也要加1，这样才能使新行优先级最高。
否则有可能与其他行的计数同为0，下次可能又被换出，而旧行却一直保留在缓存。
这是从缓存设计实验中发现，刚开始没注意到上面这点，出现BUG后去跟踪缓存行的字段才发现有个缓存行常驻缓存。

LFU

Least Frequently Used
高强次数，统计次数，换算最少的。

写回

（命中）先更改缓存，弹出缓存时再写回到主存。

直写

（命中）更改缓存并直接写回

写分配

（不命中）往回时也分配给缓存

非写分配

（不命中）往回时不分配给缓存

存储器山

CSAPP Homework 6.45
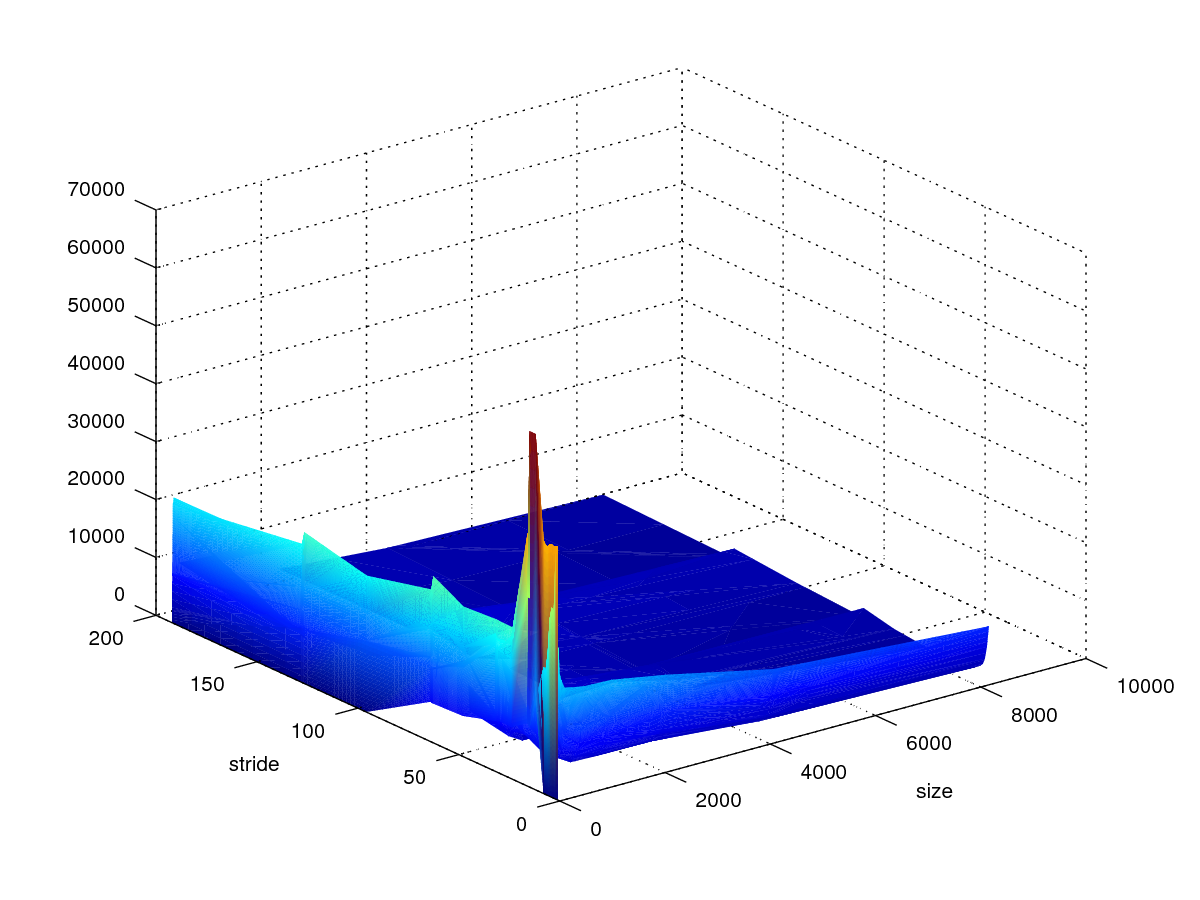
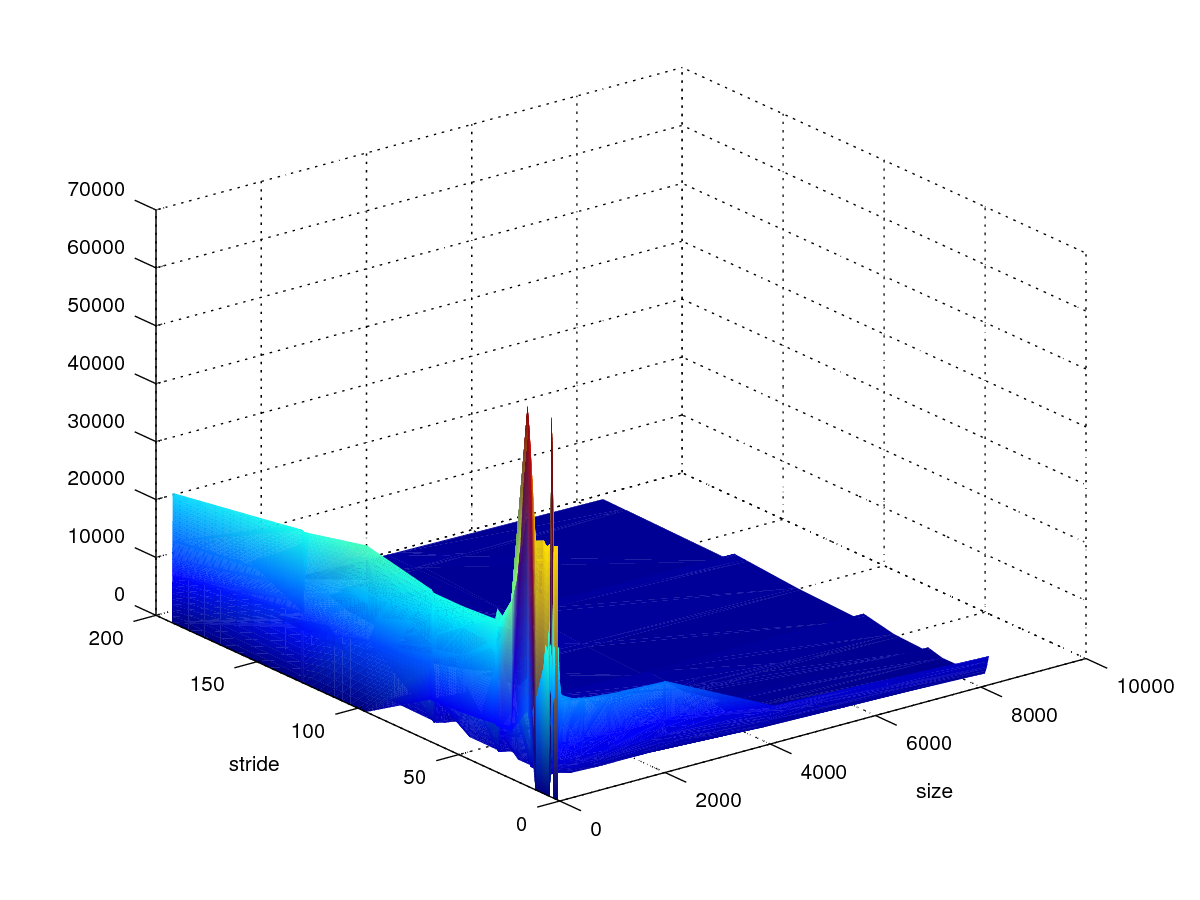
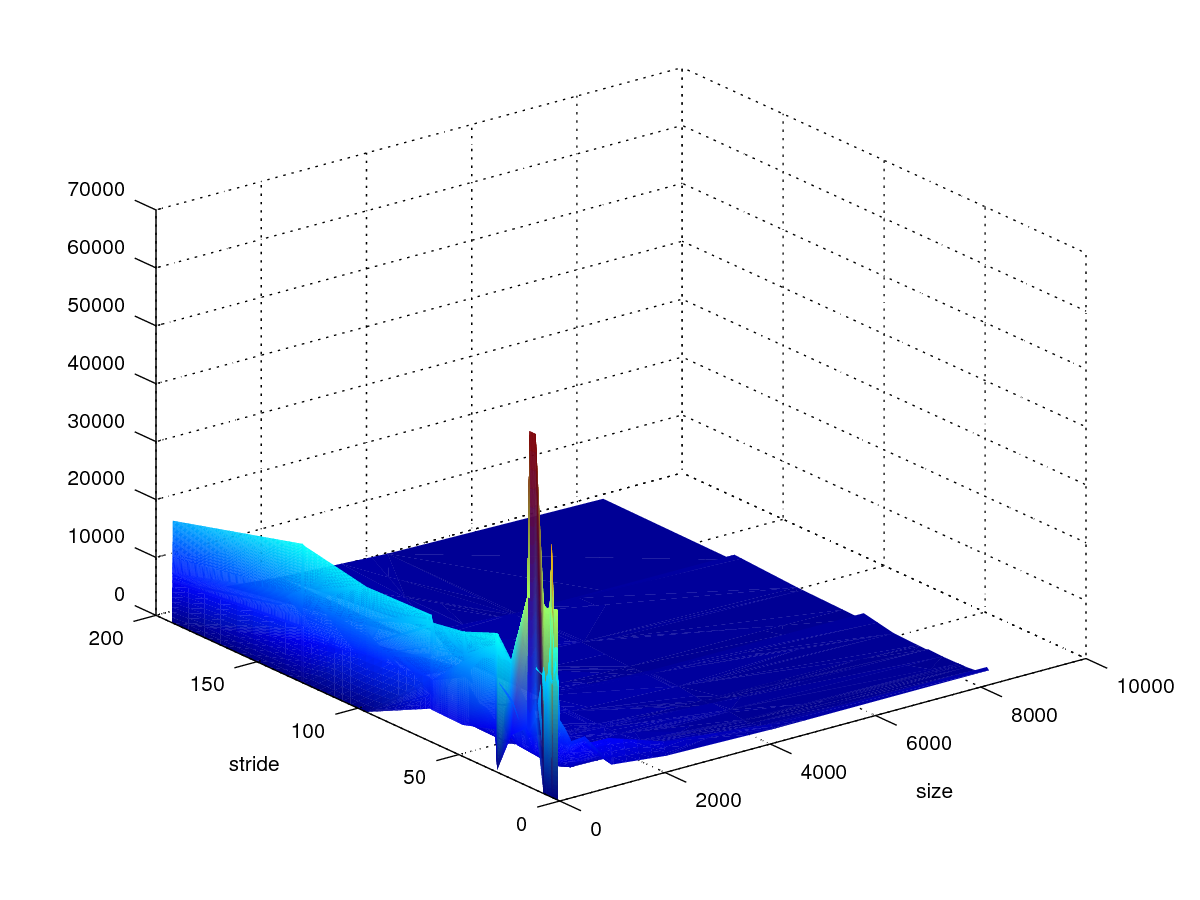
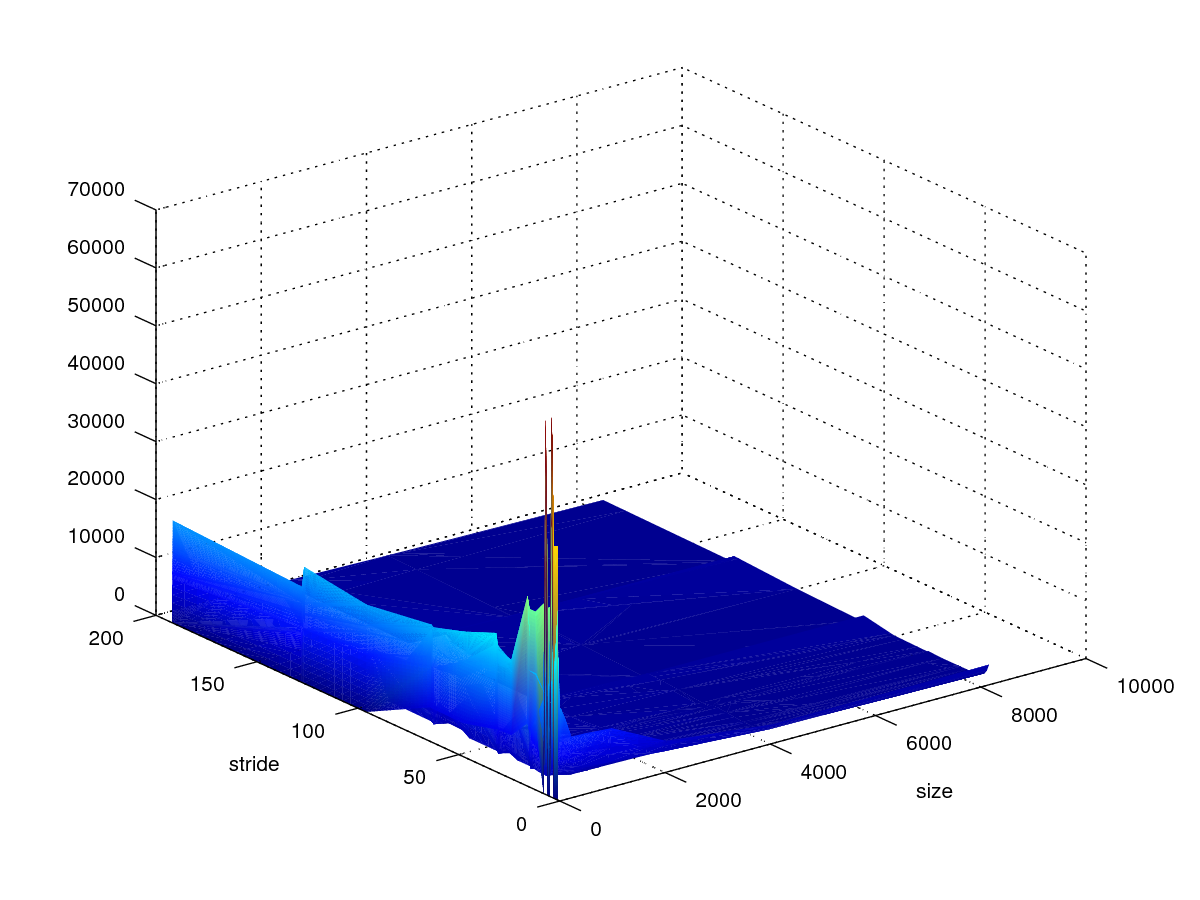
存储器山1 存储器山2 存储器山3 存储器山4
x轴size(KB)，y轴stride。
图1读取数据
图2存储数据
图3散取整存
图4整取散存
lscpu

程序优化

原程序，矩阵逆转。

void transpose(int * dst, int * src, int dim)
{
    int i, j;
    for (i = 0; i < dim; i++)
    for (j = 0; j < dim; j++)
    dst[ j*dim + i ] = src[ i*dim + j ];
}

读写变换

void transpose1(int* dst, int* src, int dim)
{
   // for中的i j对调
   for ( j = 0; j < dim; j++ )
       for ( i = 0; i < dim; i++ ) {
           dst[j*dim + i] = src[i*dim + j];
       }
}

x是dim，y是把原函数的时钟周期数减transpose1的。灵感来自存储器山中图3图4
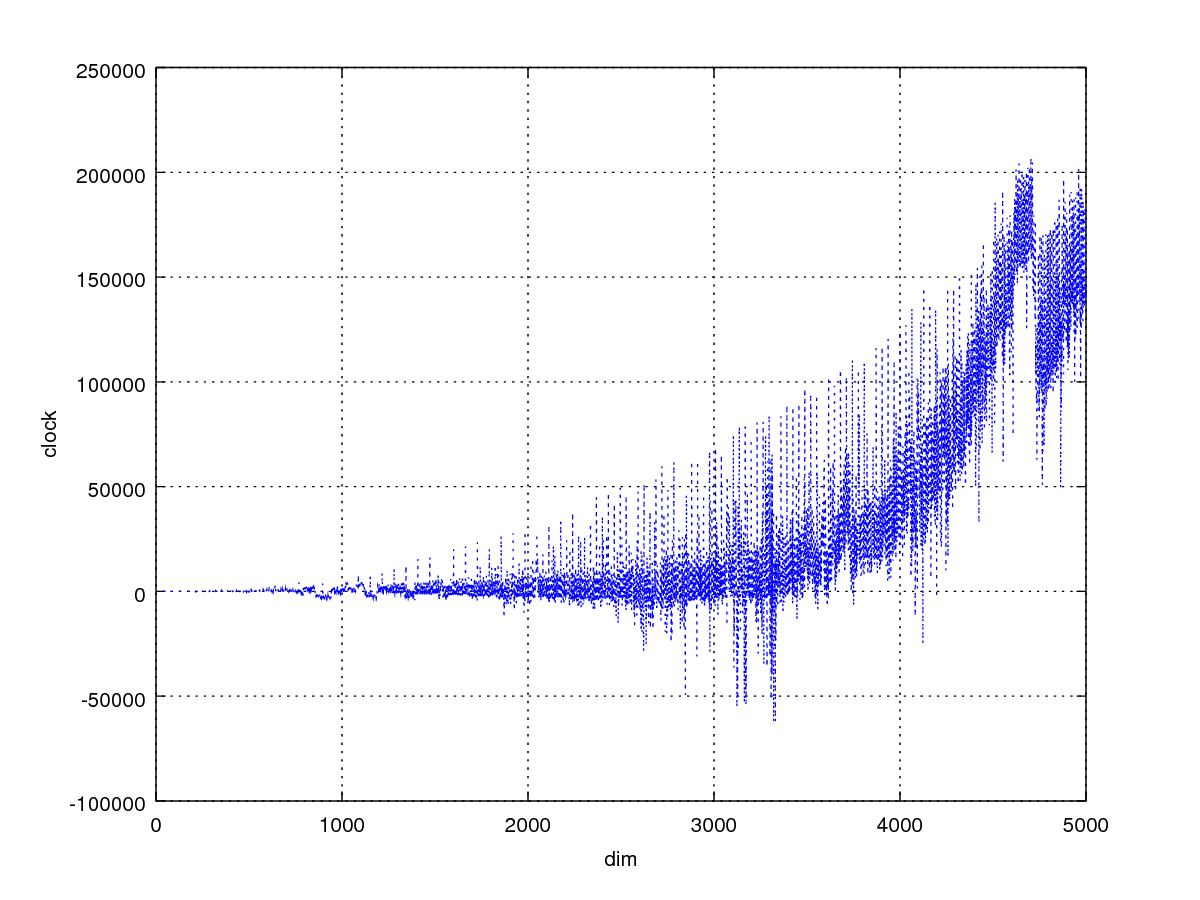
transpose5

循环展开

void transpose2(int *dst, int *src, int dim)
{
	int i, j;

	for ( i = 0; i < dim; i++ ) {
		for ( j = 0; j < dim-1; j+=2 ) {
			dst[j*dim + i] = src[i*dim + j];
			dst[(j+1)*dim + i] = src[i*dim + j+1];
		}
		for ( ; j < dim; j++ )
			dst[j*dim + i] = src[i* dim + j];
	}
}

原函数减transpose2
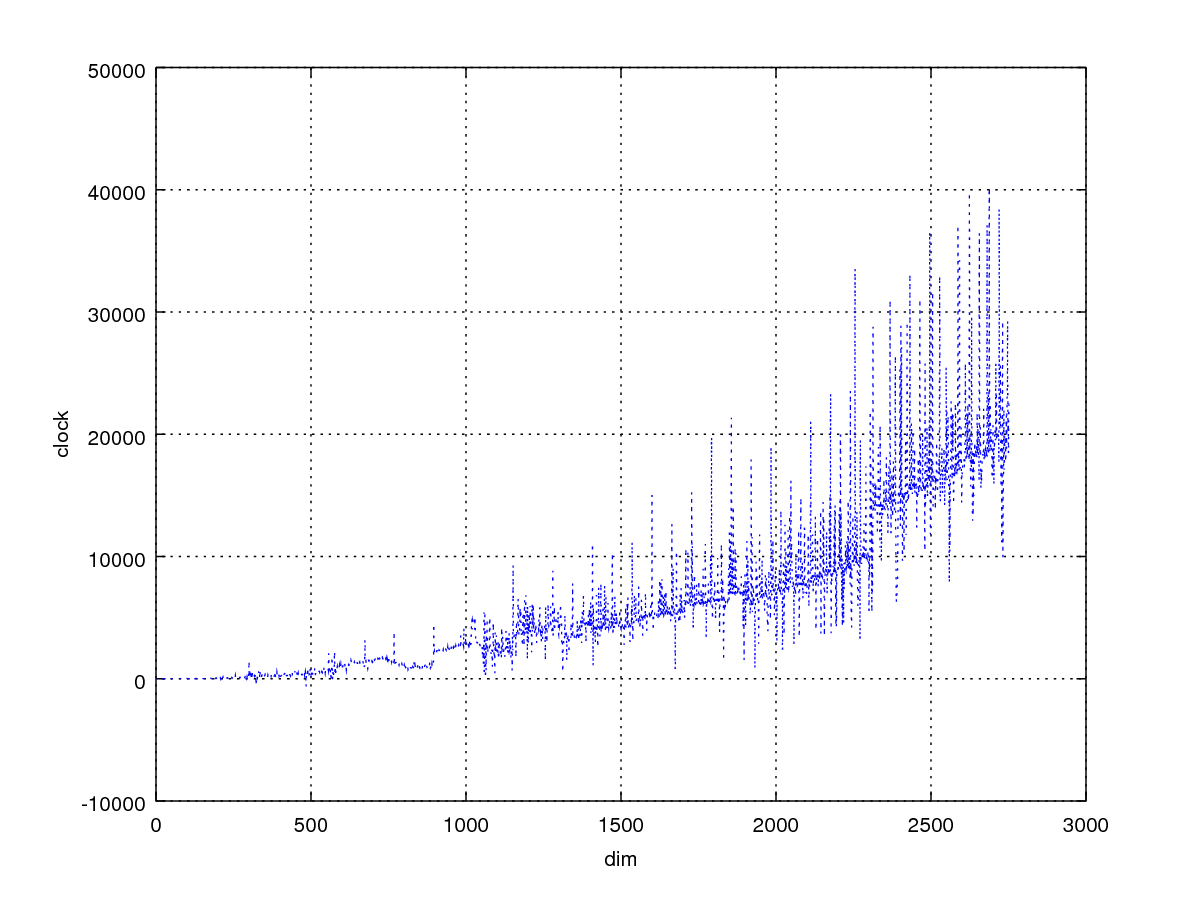
transpose6

结合

综合transpose1和transpose2

void transpose3(int *dst,int *src,int dim)
{
    int i, j;
    // 对调
    for ( j = 0; j < dim; j++ ){
        for ( i = 0; i < dim-1; i+=2 ){
            dst[j*dim + i] = src[i*dim + j];
            dst[j*dim + i+1] = src[(i+1)*dim + j];
        }
        for ( ; i < dim; i++ ){
            dst[j*dim + i] = src[i* dim + j];
        }
    }

}

把2的减去3的，得出下图，transpose3优化效果并没有多大长进。
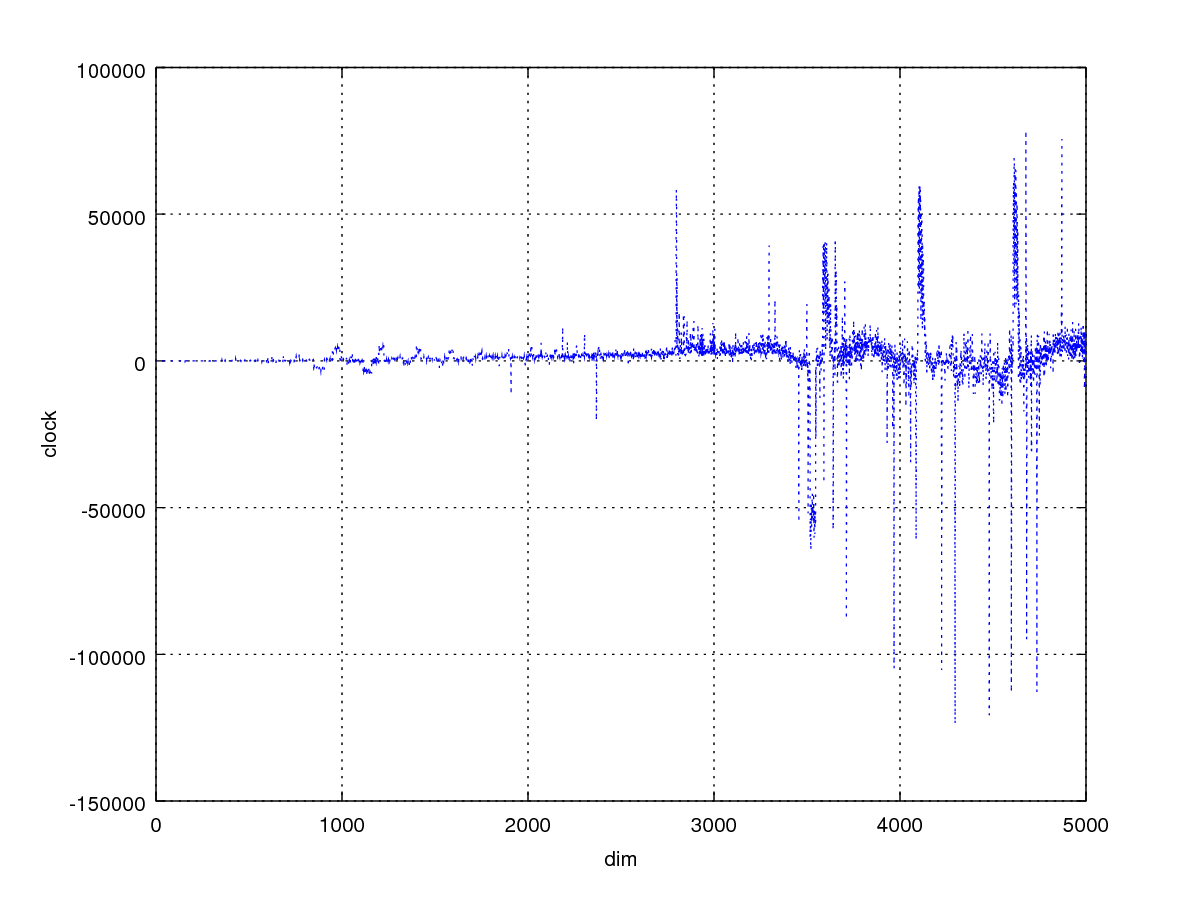
transpose7

调整缓存块

试想，可能是循环展开的次数不够，换4次展开试试。但有两个变换：

void transpose4(int* dst, int* src, int dim)
{
	int i, j;
    // 块为1*4结构
	for ( i = 0; i < dim; i++ ) {
		for ( j = 0; j < dim-3; j+=4 ) {
			dst[j*dim + i] = src[i*dim + j];
			dst[(j+1)*dim + i] = src[i*dim + j+1];
			dst[(j+2)*dim + i] = src[i*dim + j+2];
			dst[(j+3)*dim + i] = src[i*dim + j+3];
		}
		for ( ; j < dim; j++ )
			dst[j*dim + i] = src[i*dim + j];
	}
}

void transpose5(int* dst, int* src, int dim)
{
    int i, j, ii, jj, i_;
    int Dim = dim*2;
    // 块为2*2结构
    for(i = 0, ii = 0; i < dim-1; i += 2, ii += Dim)
    {
        for(j = 0, jj = 0; j < dim-1; j += 2, jj += Dim)
        {
            dst[jj + i] = src[ii + j];
            dst[jj+dim + i] = src[ii + j+1];
            dst[jj + i+1] = src[ii+dim + j];
            dst[jj+dim + i+1] = src[ii+dim + j+1];
        }
    }
    i_ = i;//j
    for(i = 0; i < dim; i++)
        for(j = i_; j < dim; j++)
            dst[j*dim + i] = src[i*dim + j];
    for(i = i_;i < dim;i++)
        for(j = 0;j < i_;j++)
            dst[j*dim + i] = src[i*dim + j];
}

4减5,得出下图，果然2*2效果好，如果展开次数越大可能就越明显。
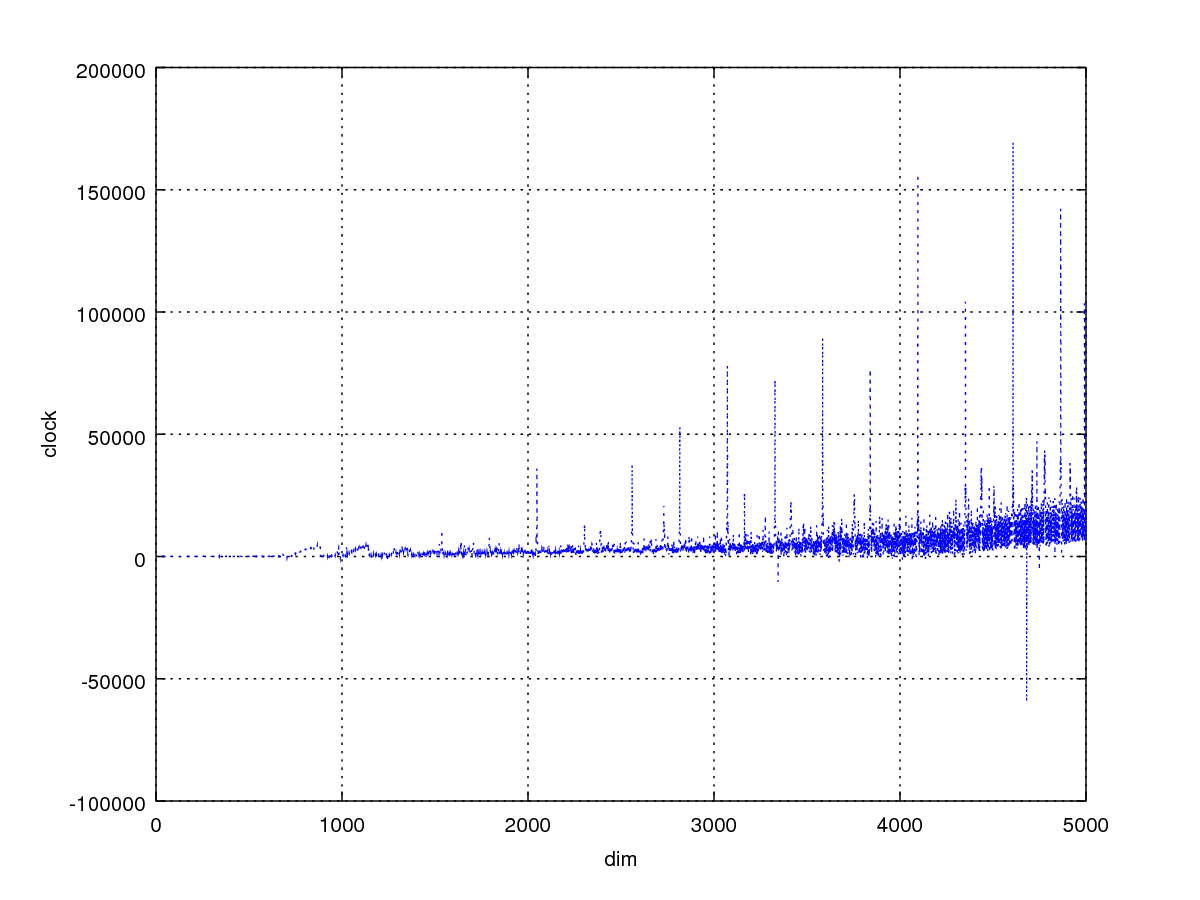
transpose8

再结合

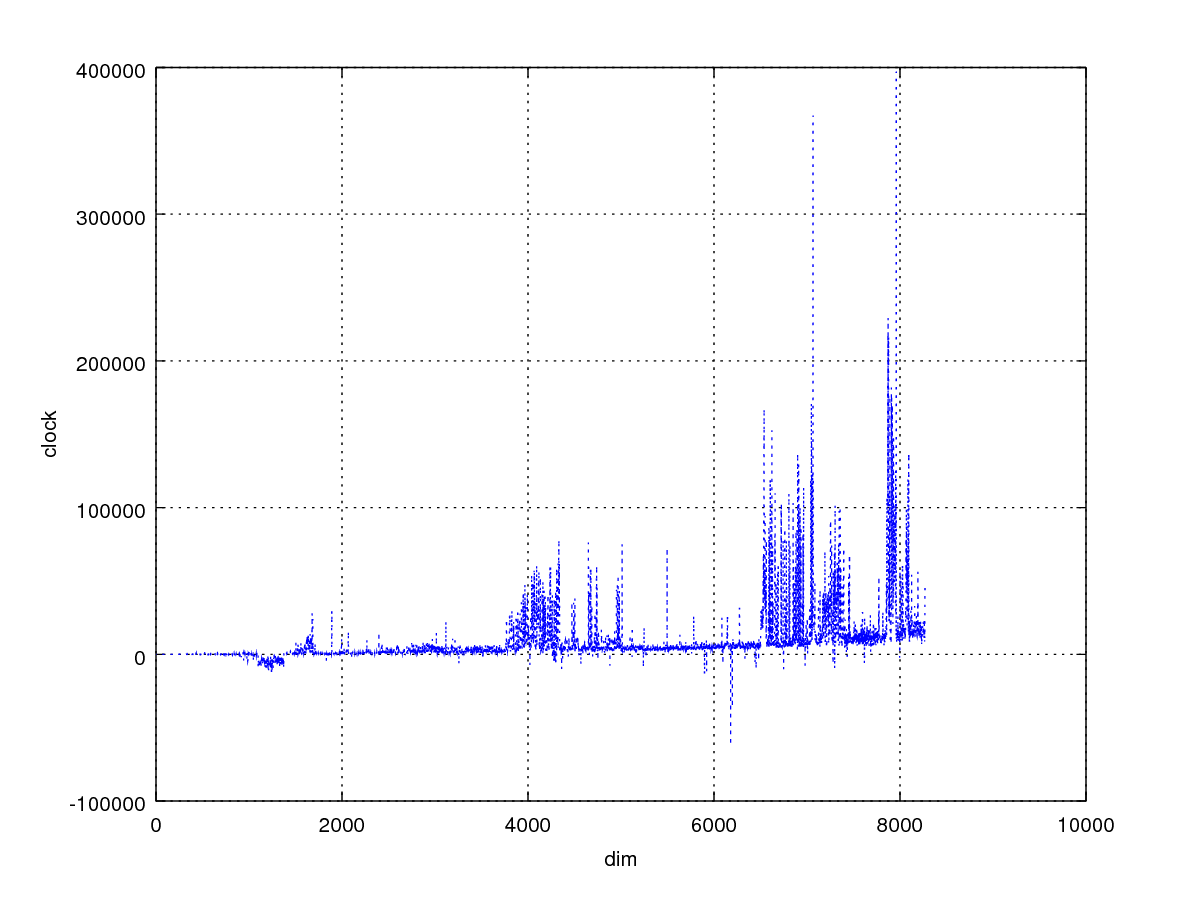
前面结合是循环2次展开，对比读写命中的性能差异，这里采用16次展开，4x4结构。
可以看出，差距有点大了，可以粗略推断写命中更有利于提高性能。
测这个很费时，故不再研究循环展开多少次最合适。
transpose9

总结

transpose1： 写命中 比 读命中 更有利于提高性能
transpose2： 1x2结构展开，性能提高
transpose3： transpose1+transpose2，效果不佳。
———————————–
transpose4： transpose2改成4次展开,1x4结构
transpose5： transpose4变成2*2结构
———————————–
transpose6： 16次展开，4x4结构,读命中。
transpose7： 16次展开，4x4结构,写命中。

CSAPP笔记（六） 存储器层次结构

RAM