CSAPP笔记（五）优化程序性能

编译器

局限性

存储别名的使用

void func1(int *xp, int *yp){
    *xp += *yp;
    *xp += *yp;
}
void func2(int *xp, int *yp){
    *xp += 2**yp;
}

如果编译器把func1优化成func2，当xp等于yp时…

函数调用

int f();
int func1() {
    return f() + f() + f() + f();
}
int func2() {
    return 4*f();
}

如果编译器敢把func1优化成func2，当f定义如下时…

int counter = 0;
int f() {
    return counter++;
}

若把f内联到func1中，

int counter = 0;
int func1in() {
    int t = counter++;
    t += counter++;
    t += counter++;
    t += counter++;
    return t;
}

GCC能优化如下

int func1opt() {
    int t = 4 * counter + 6;
    counter = t + 4;
    return t;
}

程序示例

待优化的程序

 #define IDENT 1
 #define OP *
typedef struct {
    long int len;
    data_t * data;
}vec_rec, * vec_ptr;
vec_ptr new_vec(long int len) {

    vec_ptr result = (vec_ptr) malloc(sizeof(vec_rec));
    if (!result)
        return NULL;
    result -> len = len;

    if (len > 0) {
        data_t *data = (data_t*) calloc(len, sizeof(data_t));
        if (!data) {
            free((void*) result);
            return NULL;
        }
        result -> data = data;
    } else
        result -> data = NULL;
    return result;
}
int get_vec_element(vec_ptr v, long int index, data_t* dest) {
    if (index < 0 || index >= v -> len)
        return 0;
        * dest = v -> data[index];
    return 1;
}
long int vec_length(vec_ptr v) {
    return v -> len;
}
void combine1(vec_ptr v, data_t* dest) {
    long int i;
    * est = IDENT;
    for (i = 0; i < vec_length(v); i++) {
        data_t val;
        get_vec_element(v, i, &val);
        * dest = * dest OP val;
    }
}

代码移动

Step 1

 #define IDENT 1
 #define OP *
void combine2(vec_ptr v, data_t * dest) {
    long int i;
    long int length = vec_length(v);

    * dest = IDENT;
    for (i = 0; i < length; i++) {
        data_t val;
        get_vec_element(v, i, &val);
        * dest = * dest OP val;
    }

}

减少调用

Step 2

 #define IDENT 1
 #define OP *
typedef struct {
    long int len;
    data_t * data;
}vec_rec, * vec_ptr;
data_t * get_vec_start(vec_ptr v){
    return v->data;
}
void combine3(vec_ptr v, data_t * dest) {
    long int i;
    long int length = vec_length(v);
    //直接定位到数据结构的主体区
    data_t * data = get_vec_start(v);
    * dest = IDENT;
    for (i = 0; i < length; i++) {
        //基于前面的定位去访问元素
        * dest = * dest OP data[i];
    }
}

当把编译器的优化等级调到2时会发现，下面注释的movss被优化掉了，
也就是for中的第个dest并没有访存，而是直接用上次循环的结果，也就是第21行的。

 # gcc -S combine.cpp -O2
 # for循环的汇编代码
 17 .L2:
          # movss   (%rsi), %xmm0
 18         mulss   (%rdi), %xmm0
 19         addq    $4, %rdi
 20         cmpq    %rax, %rdi
 21         movss   %xmm0, (%rsi)
 22         jne     .L2
 23         rep ret

存储别名的使用是指编译器不知两个别名是否指向同一地址，而这里肯定是同一地址。

减少访存

Step 3

 #define IDENT 1
 #define OP *
void combine4(vec_ptr v, data_t * dest){
    long int i;
    long int length = vec_length(v);
    data_t * data = get_vec_start(v);
    data_t acc = IDENT;
    for (i = 0; i < length; i++) {
        acc = acc OP data[i];
    }
    * dest = acc;
}

由于存储别名的使用，编译器并不会把combine3优化成combine4，
因为combine3中的dest是完全有可能指向data[i]，也就是说v累乘的结果可能保存在v的某个元素中
如果错误地优化了…

处理器

整体框图

处理器

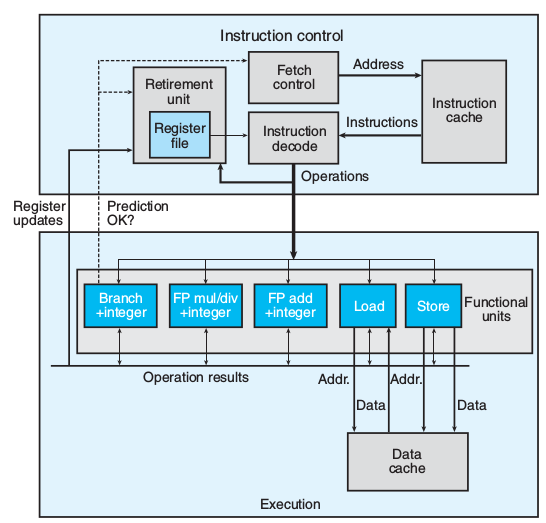
退役单元(Retirement Unit): 记录正在的执行的指令
指令译码后会传送到退役单元的队列中，等待分支预测赤决定是否写寄存器文件
PIPE中E是根据e_con和icode传送信息到D
操作结果(Operation results): 指令间转发数据寄存器重命名(register renaming)译码时，某指令要更新寄存器r，则产生（r,t）标记入表(renaming table)。
后续指令要调用r时会在译码时带上t作为源操作数(operand value)进入执行单元。
前指令得出结果v，带t指令会直接引用v
PIPE中是在译码时被动等待前指令传回数值，不回传就卡在那里不走了
而这里是在执行阶段是主动调用

抽象模型

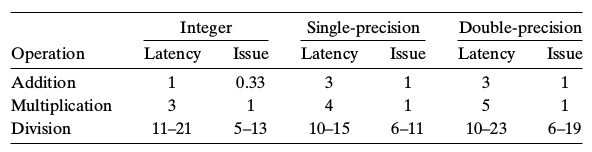
延迟(Latency)：执行一条指令所需周期
发射(Issue)：两条指令间间隔
发射为1说明，说明每个周期都执行一条指令，完全流水线化
加法0.33是因为硬件上有3个加法运算单元

for (i = 0; i < length; i++) {
    acc = acc * data[i];
}

.L488:
    mulss (%rax,%rdx,4), %xmm0
    addq $1, %rdx   //i++
    cmpq %rdx, %rbp  //i < length
    jg .L488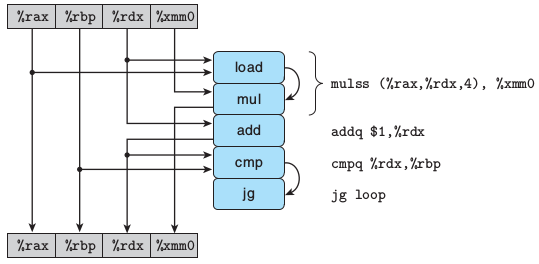

数据流图
在一个循环中，乘和加数据不相关，乘和加的指令流水可近似看成乘和加并行

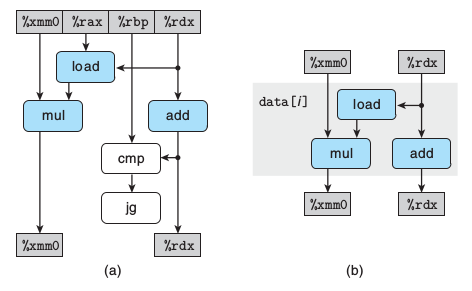
跳转指令不影响数据流，忽略不计。关键路径在于乘法运算

f(x)是关于x的degree次多项式，a是各项系数，poly求f(x)
double poly(double a[], double x, int degree){
    long int i;
    double result = a[0];
    double xpwr = x;
    for (i = 1; i <= degree; i++) {
        result += a[i] * xpwr;
        xpwr = x * xpwr;
    }
    return result;
}

如果仿照上面画出流程图，显然三条主线
1 result -> result
2 xpwr -> xpwr
3 临时寄存器 -> 临时寄存器
其中临时寄存器存放 a[i]* xpwr 的结果
两个乘法数据不相关，但result+却依赖乘法结果。
其实result+完全可以推迟到下个循环，如下：

r=0
for{
    result += r;
    r = a[i] * xpwr;
    xpwr = x * xpwr;
}
result += r;

3条主线中，第二个乘法为关键路径，时间(5)最紧，加法时间(3)最松，也就是说乘法是不停运算，而加法有两个周期休息，两个乘法数据不相关，流水并行，完全可以视为一个。

再看一代码

 # 同样求f(x)，用Horner法迭代分离x
 # a0 + x(a1 + x·a2))
double polyh(double a[], double x, int degree){
    long int i;
    double result = a[degree];
    for (i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

这种运算无解，result->result是没法等到下轮循环再计算
时间（5+3）
由此可以，减少运算并不一定会提高性能，降低运算的相关性也很重要

程序变换

循环展开

只提高了整数运算性能

 #combine5
//2次展开
for (i = 0; i < length/2; i+=2) {
    acc = (acc OP data[i]) OP data[i+1];
}
//扫尾
for{}

OP对应的延时如下

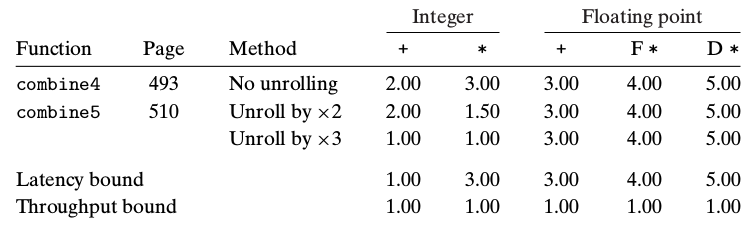
发现循环展开对浮点数运算没有有效果。看下图，浮点数运算的关键路径在于左侧
每轮OP运算必须等到上轮所有OP结束才能开始，这样就成串行了。
但整数运算性能居然提高了，这是因为GCC的优化，后面会解释
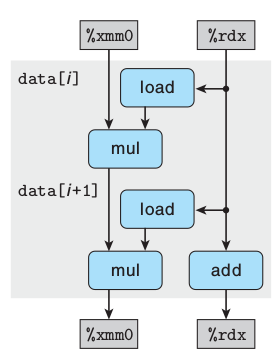
浮点循环展开

多路并行

整数和浮点都提高了

 #combine6
for (i = 0; i < length/2; i+=2) {
    acc0 = acc0 OP data[i];
    acc1 = acc1 OP data[i+1];
}

多路并行
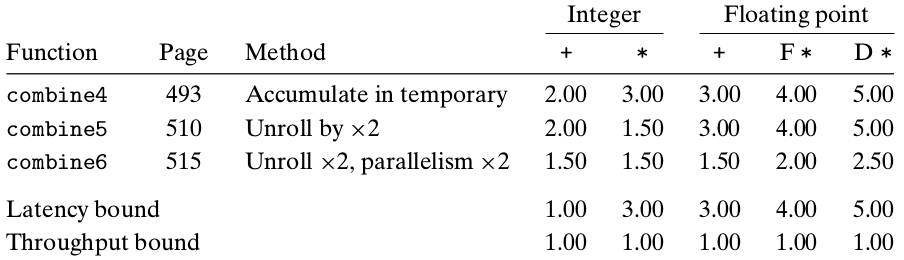
补码乘加是有结合性的，但是浮点因为溢出的问题就没有结合性，但并行计算的准确性并不一定比顺序计算的差，这个不好说。更多情况下，运算性能更重要。

结合变换

整数和浮点都提高了

 #combine7
for (i = 0; i < length/2; i+=2) {
    acc = acc OP (data[i] OP data[i+1]);
}

结合变换
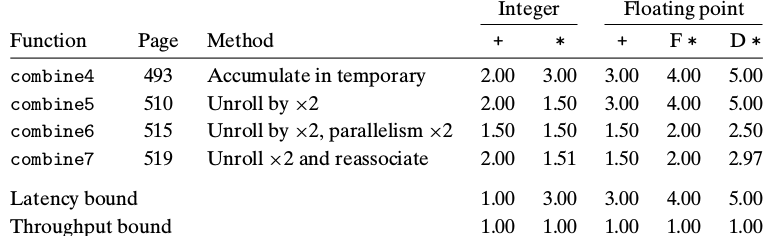
这里可以想像有双核CPU，A负责acc的op运算，B负责data的op运算。以乘法为例，B每3个周期把结果写入寄存器，A每3个周期读寄存器。B中的关键路径是乘法运算，周期为3，两次访存只要2个周期，完全可以在运算时同时进行访存，读取下个循环要用的数据。访存单元还有一个周期的休息时间，而乘法单元却一直在跑。然而这里并没有双核，如果第二个OP先行一个循环，两个乘法数据就不相关，第一个OP关联的是第二个OP上一次循环的结果，这个无所谓，这样本次循环就完全可以流水，效果同双核并行，也就是说下面两行的代价是一样，寄存器充足的情况下应尽量循环展开，正所谓事半功倍。

acc = acc OP (data[i] OP data[i+1]);
acc = acc OP data[i];

而combine5浮点运算性能差的关键原因在于两个OP都需要acc参与计算，也就是说第二轮循环一定要等到第一轮中OP 全部运算结束才能开始，没法流水达到并行，执行一个OP时另一个只能干等着。
但combine5中整数运算性能提高了，这是因为GCC把整数运算的优化成combine7形式，
而浮点数运算没有结合性，GCC不敢优化，所以combine7这里需要程序员手动对浮点数进行结合变换。

//r,x,y,z均为浮点数，浮点乘法延迟为5
r = ( (rx) y )z; // 3/3*5  与r相关的运算占3/3
r = ( r(xy) )z;  // 2/3*5
r = r( (xy)z );  // 1/3*5
r = r( x(yz) );  // 1/3*5
r = (rx) (yz);   // 2/3*5
...

分支预测

void merge(int src1[], int src2[], int dest[], int n) {
    int i1 = 0;
    int i2 = 0;
    int id = 0;
    while (i1 < n && i2 < n) {
        if (src1[i1] < src2[i2])
            dest[id++] = src1[i1++];
        else
            dest[id++] = src2[i2++];
    }
    while (i1 < n)
        dest[id++] = src1[i1++];
    while (i2 < n)
        dest[id++] = src2[i2++];
}

三个while都只会错一次，而if不好说，第一个while汇编如下，入口.L2

.L8:
	movl	28(%esp), %ebx
	addl	$1, %eax # i1++
	movl	%edi, -4(%ebx,%ecx,4) # src1[i1]->dest[id]
.L5:
	addl	$1, %ecx # id++
.L2:
	cmpl	%esi, %eax  # n <= i1
	jge	.L1
	cmpl	%esi, %edx  # n <= i2
	jge	.L1
	movl	24(%esp), %ebx
	movl	0(%ebp,%eax,4), %edi # src1[i1]
	movl	(%ebx,%edx,4), %ebx  # src2[i2]
	cmpl	%ebx, %edi # 2 > 1
	jl	.L8
	movl	28(%esp), %edi # dest
	addl	$1, %edx  # i2++
	movl	%ebx, -4(%edi,%ecx,4) # src2[i2]->dest[id]
	jmp	.L5

改成条件转移

int v1 = src1[i1];
int v2 = src2[i2];
int taken = v1 < v2;
dest[id++] = taken ? v1:v2;
i1 += taken;
i2 += 1-taken;

.L9:
	cmpl	%ebx, 32(%esp)
	jle	.L5
.L6:
	movl	(%edi,%ebx,4), %eax # 1->
	xorl	%edx, %edx
	cmpl	%eax, 0(%ebp,%ecx,4) # 左1右2
	cmovle	0(%ebp,%ecx,4), %eax # 右>=左时mov
	setl	%dl # 左<右时dl为1
	addl	$4, %esi
	movl	%eax, -4(%esi)
	movl	$1, %eax
	addl	%edx, %ecx # 2
	subl	%edx, %eax # (1-taken)
	addl	%eax, %ebx # 1
	cmpl	%ecx, 32(%esp)
	jg	.L9
.L5:
    # 剩下的两个while

jg和jle是while (i1 < n && i2 < n)逻辑，前后向分支，谁的地址小就先执行谁，L5最大，故只会猜错一次。初看感觉很奇怪，为啥要把两个分支预测一个头一个尾。如果都放头，尾部要多个jmp跳头；如果都放尾部，”&&”逻辑比较麻烦，如果while中是“或”逻辑就比较好搞。

存储器

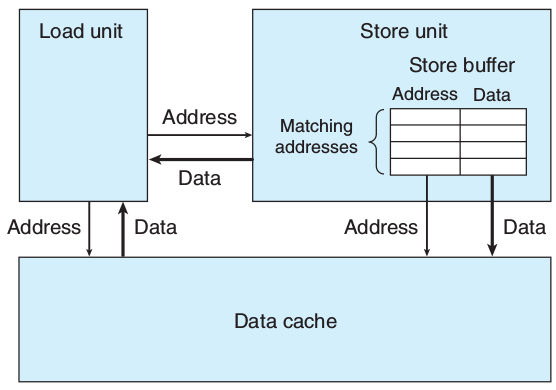
存储与加载
Load前会先检查Store buffer，有则取之。

void psum1(float a[], float p[], long int n){
    long int i;
    p[0] = a[0];
    for (i = 1; i < n; i++)
        p[i] = p[i-1] + a[i];
}

如果不考虑编译器优化，存储与加载数据相关，需要在存储的同时也保存到寄存器中，变动如下。
实际gcc -O3也能达到此效果。

temp = p[0]=a[0];
for (int i = 1; i < n; i++) {
    int val  = temp+a[i-1];
    p[i] = val;
    temp = val;
}

家庭作业

void inner4(vec_ptr u, vec_ptr v, data_t * dest){
    long int i;
    int length = vec_length(u);
    data_t * udata = get_vec_start(u);
    data_t * vdata = get_vec_start(v);
    data_t sum = (data_t) 0;
    for (i = 0; i < length; i++) {
        sum = sum + udata[i] * vdata[i];
    }
    * dest = sum;
}

以浮点为例，可以先想像双核CPU，A负责sum+，B负责data*。浮点乘法需要3个周期，最好情况下，A每3个周期向寄存读取个数进行累加。关键在于B能每3个周期提供一个数吗？B中两次访存需要两个周期，但乘法5个周期，即使在乘法运算的同时访存5次也没啥鸟用，乘法单元5个周期才能产生一个结果。故只能扔给其他核去运算，假如有C核一起参与乘法运算，乘法运算周期缩短到5/2，完全可以在3个周期内给A提供结果。当然，这里A和B一个加一个乘，运算没有冲突，完全可以合并成一个核，BC的两个乘法数据不相关，可以在一个核中通过流水来实现并行，也就是说BC是流水线中相邻的两个指令。加法运算是数据相关的，谁也救不了，无解。
对于整数，A中加法周期1，但B的关键在于访问没法并行，只能串行，借助C的情况下最快也只能2个周期产生一个数。同样ABC可合并。
其实访存串行跟并行一样的，因为它只有1个周期，指令流水间隔就是1个周期。
Solution:
5.15 D：浮点乘法流水并行，关键路径在加法。

循环2次展开，2次并行累加
void inner4(vec_ptr u, vec_ptr v, data_t * dest){
    for (i = 0; i < length/2; i+=2) {
        sum = sum + (udata[i] * vdata[i]+udata[i+1] * vdata[i+1]);
    }
}

对于整数，循环次数减半，但B周期翻倍。因为访存次数已经由length定死了，并且串行，所以for组合无论怎么变都没用。
对浮点循环次数减半，B周期由2变4成为关键路径，故关键路径由3变4。这样跟整型运算的周期变成相同了。
Solution:
5.16 A：不能并行访存
5.16 B：浮点运算没有结合律，如果for中没加括号，编译器并不会自动优化。
5.17 B：IA32寄存器太少
5.18 : 从5.17中看出，循环3次展开时周期理应为6，实际为8，寄存器的使用达到上限。故应该循环2次展开，2次并行累加。

void * basic_memset(void * s, int c, size_t n){
    size_t cnt = 0;
    unsigned char * schar = s;
    while (cnt < n) {
        * schar++ = (unsigned char) c;
        cnt++;
    }
    return s;
}

CSAPP笔记（五） 优化程序性能

编译器

局限性